深度学习花书笔记（待更新中）

现存疑问

数学知识

线性代数

生成子空间

一组向量的生成子空间：原始向量线性组合能抵达的点的集合。

用于判断方程是否有解。

范数

${ L^p }$ 范数定义：
$$
\left | x_p \right | = \left (\displaystyle\sum_{i}|x_i|^p \right )^{\frac{1}{p}}
$$
${ L^0 }$范数：向量中非零元素的个数。

${ L^1 }$范数：向量中所有元素绝对值之和。

${ L^2 }$范数（欧几里得范数）：向量元素绝对值的平方和再开方，计算向量长度。

${ Frobenius}$范数：所有元素的平方和再开方，衡量矩阵大小。
$$
{\left | A \right |}F = \sqrt{\sum{i,j}A_{i,j}^{2} }
$$
${ L^ \infty }$范数：向量中所有元素中最大的绝对值。

奇异值分解

特征分解：
$$
A = Vdiag(\lambda )V^{-1}
$$
奇异值分解：
$$
A = UDV^T
$$

${ A_{m\times n}, U_{m\times m}正交, V_{n\times n}正交,D}$为对角矩阵但不一定是方阵。

Moore-Penrose伪逆

方程：
$$
Ax=y
$$
左乘左逆B：
$$
x=By
$$

$$
A^{+}=VD^{+}U^{T}
$$

${D^{+}}$是对角矩阵D的非零元素取倒数再转置得到的。

迹运算

Tr(A)表示矩阵对角元素之和。描述${ Frobenius}$范数：
$$
\left | A \right |_F = \sqrt{Tr\left (AA^{T}\right )}
$$
循环转置保持一致：
$$
Tr(ABC)=Tr(CAB)=Tr(BCA)
$$

概率论

delta函数：${\delta \left (x\right )}$，广义函数，除0以外处处为0，积分为1。

sigmoid函数：
$$
\sigma \left ( x\right )=\frac{1}{1+{e}^{-x}}
$$

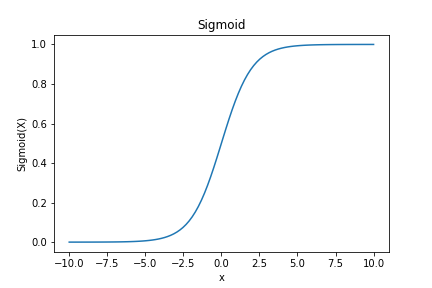
非负，绝对值大时饱和，值域(0,1)。

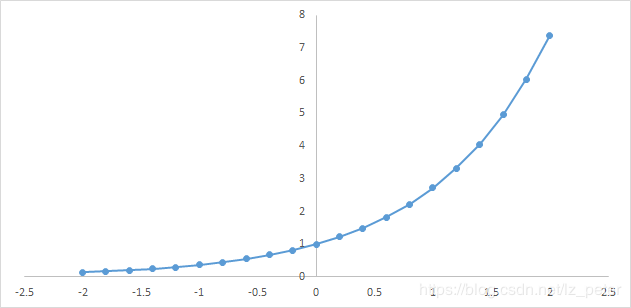
softmax：
$$
\zeta \left ( x\right )=log\left ( 1+{e}^{x}\right )
$$
软化的max(0,x)函数，非负。

贝叶斯规则：
$$
P\left ( x\mid y\right )=\frac{P\left ( x\right )P\left ( y\mid x\right )}{P\left ( y\right )}
$$

信息论

一个事件的自信息：
$$
I\left ( x\right )=-logP\left ( x\right )
$$
香农熵（信息熵）：量化整个概率分布中不确定性总量。概率的对数（logP(x)）的均值。
$$
H\left ( x\right )=-E_{x\sim P}\left [ logP\left ( x\right )\right ]
$$

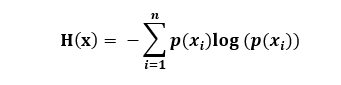
KL散度：衡量两个分布的差异。

$$
D_{KL}\left ( P\parallel Q\right )=E_{x\sim P}\left [ log\frac{P\left ( x\right )}{Q\left ( x\right )}\right ]
$$
交叉熵：
$$
H\left ( P,Q\right )=-E_{x\sim P}\left [ logQ\left ( x\right )\right ]
$$

$$
H\left ( P,Q\right )=H\left ( P\right )+D_{KL}\left ( P\parallel Q\right )
$$

针对Q最小化交叉熵==最小化KL散度，因为Q不参与H(P)。

数值计算-KKT

上溢：大量级的数被近似为无穷大。

下溢：接近0的数被四舍五入为0。

病态条件：输入被轻微扰动而迅速改变的函数。会导致舍入误差很大。

1.梯度下降算法。一阶：雅可比矩阵；二阶：海赛尔矩阵。

步长：学习率。

2.牛顿法。

凸优化：针对凸函数的优化，易成功。

3.约束优化：KKT方法

参考教程

区分等式约束和不等式约束，列方程：方程对变量求导的梯度为0，等式约束和不等式约束（相当于方程对参数的求导），不等式约束的参数k及其与不等式的乘积均非负（互补松弛性）

机器学习基础

机器学习总的来说就是一个训练参数的过程。此外，大部分机器学习算法都有必须在学习算法外设定的超参数。例如，线性回归中的参数是权重和偏置。

学习算法

学习：经验E改进后，模型在任务T上由性能度量P衡量的性能有所提升。

任务T：处理样本，学习特征。

性能度量P：准确率/错误率。样本划分训练集、验证集和测试集，它们是属于同一分布（数据生成分布）的独立变量。验证集用于及时发现模型或者参数的问题，快速调参，选择超参数，总而言之仍然是帮助训练的。

经验E：机器学习算法分为有监督和无监督。无监督的样本：数据。有监督的样本：（标签/目标，数据）。

表示数据集：设计矩阵。

容量

泛化：在未观测到的数据上表现良好。
训练误差：在训练集上的误差。
测试误差（泛化误差）：在测试集上的误差。
欠拟合：难以取得足够低的训练误差。
过拟合：训练误差和测试误差之间的差距过大。
模型的表示容量：模型规定，在调整参数时学习算法能从哪些函数中选择函数。有效容量可能小于表示容量（由于优化算法的不完美等）。

奥卡姆剃刀：简约原则，在同样能解释已知观测现象的假设中，应挑选“最简单”的那个。

VC维度：分类器能分类的训练样本的最大数目，度量二元分类器的容量。

训练误差和测试误差之间差距的上界随着模型容量增长而增长，随着训练样本增多而下降。

贝叶斯误差：从预先知道的真实分布预测而出现的误差。由于映射的随机，或其他变量的影响。是固定存在的误差。

最优容量点处的测试误差趋近于贝叶斯误差；训练误差在样本容量的限制下可以低于贝叶斯误差，因为算法有能力记住训练集中这些特定的样本。当训练样本增至无限大，训练误差至少增至贝叶斯误差以上。

没有免费午餐定理

没有永远最优的机器学习算法。也即没有最优的正则形式。在所有可能的数据生成分布上平均之后，每个分类算法在未事先观测的点上有相同的错误率。要针对特定任务选择算法。

正则化

正则化：修改学习算法，使其降低泛化误差而非训练误差。

学习算法受到假设空间的函数数量和这些函数的具体形式影响，只能通过增加和减少学习算法可选假设空间的函数来增减模型的容量。正则化是更一般地控制模型容量的方法，含义是我们在假设空间中可能对学习算法有偏好。

例如，加入权重衰减来修改线性回归的训练标准。带权重衰减的线性回归的最小化目标${\mathcal{J}\left ( \mathcal{w}\right ) }$是训练集上的均方误差与正则项的和，其偏好于平方范数较小的权重：
$$
\mathcal{J}\left ( \mathcal{w}\right ) =MSE_{train}+\lambda {\mathcal{w}}^{T}\mathcal{w}
$$
${\lambda}$控制偏好程度，=0时表示没有偏好，会过拟合，过大会导致欠拟合。

例如，用9阶多项式拟合2阶多项式时，偏好用更简单的模型来描述，能取得更好的效果。

超参数和验证集

超参数：难优化，或更多为不适合在训练集上学习。例如，多项式的次数，控制权重衰减程度的${\lambda}$。

如果在训练集上学习超参数，它们总是趋向于最大可能的模型容量，导致过拟合。此时需要验证集。

验证集：通常将训练数据划分为训练集和验证集，验证集用于估计泛化误差以更新超参数。

交叉验证：将数据划分为训练集和测试集，从而利用测试集求取泛化误差。

估计、偏差和方差

点估计

也称为统计量，定义宽泛，为数据提供单个“最优”预测：
$$
{\hat{\theta}}_{m}=g\left ( {x}^{\left ( 1\right )},…,{x}^{\left ( m\right )}\right )
$$
也可输入和目标变量之间关系的估计，称为函数估计。

偏差

预测值和真实值之间的差的均值。为零时称估计量为无偏。偏差在无限大时趋近零称为渐进无偏。

方差和标准差

表示估计量的变化程度。标准差是方差的平方根。

权衡偏差和方差以最小化均方误差MSE： $$ MSE=E\left [ {\left ( {\hat{\theta}}_{m}-\theta \right )}^{2}\right ]=Bias{\left ( {\hat{\theta}}_{m} \right )}^{2}+Var\left ( {\hat{\theta}}_{m} \right ) $$